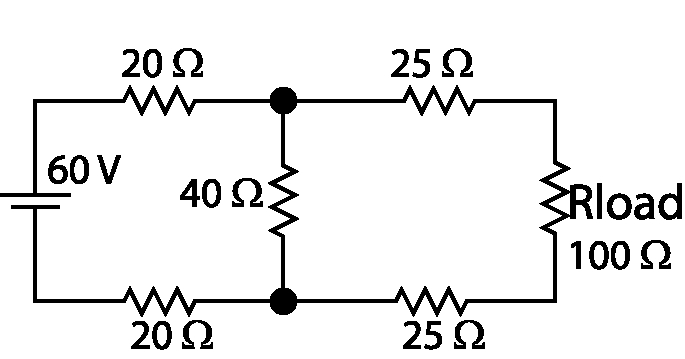
As part of the Software Engineering curriculum, I was required to take “Principles of Electrical Engineering” this semester. This is a mandatory course for all engineers at Concordia, so the class was full of people working in a somewhat unfamiliar domain. It was a tough course, but fortunately I had a good background in electromagnetism from my pure & applied science Cégep degree (Cégep is pre-university in Quebec.)
One thing I noticed while taking the class was how most students simply reduced the circuit analysis to math and never bothered to properly grok how electrical systems actually work. I was definitely guilty of this as well; I have only a very abstract notion of what capacitors actually do but know enough to blindly calculate their impedance. Indeed, some of my classmates had only a vague notion of the physical difference between voltage and current.
I’ve had to explain the basics of electricity to others once or twice in my lifetime, and I’ve come up with a rather simple analogy to do so. As a disclaimer, I’ll repeat that I’m not an electrical engineer and have only a rudimentary knowledge of electrical systems. There are many good analogies to explain how electricity works, and I happen to like this one.
 Photograph by JMUAIANWNC 3366688, License CC BY-SA 4.0
Photograph by JMUAIANWNC 3366688, License CC BY-SA 4.0
Imagine the circuit as a system of roads, and on these roads are trucks delivering watermelons. Why watermelons you ask? Because they’re delicious, don’t ask silly questions. These trucks drive around the circuit, picking up watermelons (charges) at the farms (voltage/current sources) and dropping them off at the markets (resistors.) Therefore:
- The trucks are the charge carriers, and number of trucks is analogous to the current (amperes.) In other words, a current of 10A in a systems can be viewed as having ten trucks driving around.
- The voltage (volts) is comparable to the number of watermelons. Saying the potential difference across a resistor is 40V is analogous to saying 40 watermelons were dropped off at that market.
- Resistance (ohms) is the number of watermelons per truck that need to be dropped off at the market. If a resistor has a value of 10 ohms, then each truck that passes it will drop off 10 watermelons.
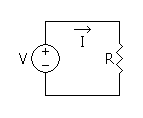
How well does this analogy hold up? It properly illustrates Ohm’s law, the quintessential electrical formula. The law states that potential difference across a resistor (V) is equal to the current (I) times the resistance (R). In other words, the number of watermelons dropped off at a market is equal to the number of watermelons per truck times the number of trucks.
As with most analogies, this is a rather gross simplification. Amperage is not actually a measure of the number of charge carriers, but rather the number of charge carriers per second. In many ways electrical charge (Coulombs) is a better analogy for the number of trucks, and amperage for a more general “flow of traffic.” Furthermore, voltage is actually defined as the amount of energy in Joules (watermelons?) per charge carrier (truck.)
Despite its flaws, I feel that the watermelon truck analogy does a better job of defining charge carriers and potential than the popular water comparison. If you have an analogy that worked for you when learning about electricity, I’d love to hear about it in the comments.







April 29th, 2008 at 12:54 am
I was fairly hopeless in the labs, everything was written out in obvious instructions (plug this here, turn this on) so my thinking was at a minimum. This was partly due to the fact that the labs were a week ahead of the lectures, so I usually had no idea what was going on.
We have to apply what we learned in ELEC275 this semester to “control systems” in the future. I’m sure that’ll be another challenging class.
April 28th, 2008 at 11:33 pm
I started off doing an electrical engineering degree.
I had a weird experience once during a project we were working on. We were making something with resistors, capacitors, diodes and an oscilloscope bla bla, as you do. We were getting some weird pattern on the oscilloscope which was nothing like we should have been getting. My partner was frantically checking each component one by one to make sure it matched the plan.
In an odd moment of clarity, I stood back and pondered it for about 5 seconds with my hand stroking my chin (totally unintentionally). I watched the oscilloscope and the pattern reminded me of capacitors.
I visually imagined behaviour of the electrons and a capacitor and imagined the behaviour if the current was flowing in the other direction. It was the weirdest problem solving I’ve ever done. I really didn’t think about it at all, my understanding of the process just naturally crystalised in my head right at that moment and spontaneously inverted itself.
In a swift ‘aha!’ moment I switched the capacitor (which we’d already checked, incorrectly) to be backwards which out looking at it’s polarity, and the oscilloscope looked exactly like it was supposed to.
That’s the only thing I got out of electrical engineering. I’ve forgotten all about capacitors and the rest now, but that moment was all that mattered.
So yeah.. understanding the physical phenomenon really is worth it.
April 29th, 2008 at 7:59 pm
This is a pretty sweet analogy. Will probably come in handy when I have to take this class in the Winter.
Back in high school, they used the analogy of water flowing through a pipe. The current was the amount of water flowing through at a given point (which should always be the same) and voltage was how fast the water was moving through the pipe, like the amount of pressure. I’m not sure how well I remember this, so forgive me if I’m wrong.
In cegep, I was pretty much guilty of blindly doing the math when it came to problems. And for theory questions, it was just writing down what sounded best.
April 30th, 2008 at 12:49 am
I actually linked to the water analogy at the bottom of my post. It works too, I suppose, but to me it doesn’t illustrate the idea of charge carriers very well. That makes it different to introduce the idea of Coulombs and Joules later on.
I recommend Dr. Ramachandran for ELEC275 if you have the choice, mostly because he breaks it all into an easy to understand step-by-step formulas. They also have SL tutorial sessions, which I highly recommend.