I think I had best wrap up this series before I completely alienate my non-programmer readers. Firstly, I have an algorithm by fellow blogger and mathematician Tim Sell of Planet Nectarius.
[A.I Competition – Tim’s Algorithm]
What I did was get 3 values for all the empty spaces to the left, right and in front of the player. To be “in front” the empty spaces must be connected to the forward move square and it must be forward of the player. So each connected space is bounded by a rectangle to one side of the current cycle position. I then regard each rectangles emptiness value as half if the nemesis cycle is within that rectangle. Then I arbitrarily decide to move to the square which has the second highest empty space value associated with it. […] Basically the idea is to cut of the nemesis cycle from the empty space without retreating into it.
He later added:
I made a slight mistake, best explained by example: If I am getting the space that is south, the GetSpace function gets each empty square that’s below it and to the left and right recursively. What I meant it to do was to do that, but also go up again if it is still below the player’s cycle, this would let it account for spaces that go down and then up again to one side.
To reiterate, what Tim’s algorithm does is compare the amount of space connected to the three spaces adjacent to the cycle. However, it only counts the spaces contained in a rectangle defined by the cycle and the scanning direction. To illustrate:
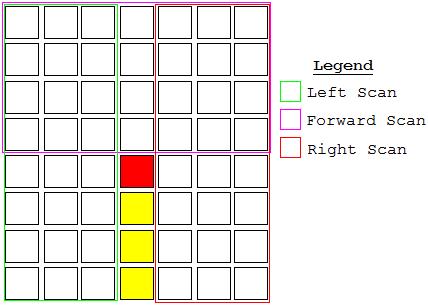
The forward scanners will only scan within the forward box, the left ones within the left box, and so on. It’s an interesting approach, but I fear that it may suffer from the same weakness as algorithm 3: doing a bad job of filling empty space slowly. Without real code to test, of course, this is mere speculation.
Lastly, I have a few wild and crazy algorithm ideas I came up with while trying to approach the problem sideways. I don’t think any of them would work particularly well, but they make good thought exercises.
- The Calculus Approach: I thought of this algorithm while working on a Numerical Methods assignment. We could send out a 90 scanners, 30 in each direction. These scanners would have semi-random behavior; they would never run into a wall if they could avoid it but would make all other turning decisions randomly. These scanners would leave walls behind themselves on cloned maps as they moved, and return their path length upon death. Once they have all died, we could take the average of their path lengths and choose to turn in the direction with the highest average. We could increase the number of scanners for a better estimation at the cost of processing time.
- The Cardinal Directions Approach: We could send out four scanners from the cycle: one that can only turn North and West, another North and East, another South and West, etc. We could then calculate the free space value for each cardinal direction using the average of the two ordinal directions: (NW+NE)/2 = N. We decide in which direction to turn based on this information.
- Average of BFS and DFS: I mentioned in my last post that a Breadth First Search and a Depth First Search estimated free space in a slightly different way. Perhaps the best solution would be to perform both and take the average, hoping that the strengths of one would cancel out the weaknesses of the other. It would involve twice as much calculation, but I think it might actually work reasonably well.
In conclusion, I would like to quickly thank Sven and William (my CS games teammates), Alexei, Andrew and Tim (for taking the time to discuss their algorithms with me), and Renaud and Thomas (for the lengthy algorithm discussions.) I learned a lot by writing this series, and am now exceptionally prepared for next year’s A.I. competition.




