Since I returned from the CS games a few weeks ago, I’ve been vigorously discussing the Tron A.I. problem with anyone who would listen. Much of this took place on the skrud.net forums, where I had a chance to debate with Alexei and Andrew of the other Concordia team. Their team tied for third place on the second day, and they had some really interesting ideas. I’ll be posting snippets of our discussion here, including the pseudocode for their algorithm.
In part 2 of this series, I wrote about how the recursive Algorithm 4 was memory intensive because it needed to clone the entire map at every step. Alexei, however, thought of a very clever way to get around this problem by implementing backtracking.
[A.I Competition – Backtracking Algorithm]
Using this algorithm, you would need to clone the map exactly once (assuming the original map cannot be modified.) In Alexei’s words:
Nothing is being cloned, because you are always operating on the same state. As it recurses in, it marks the node, and then unmarks it as it recurses out.
So if you’re in a 10-level deep recursion, you have 10 nodes marks as visited (ie the “path” you’re currently looking at). Suppose that you’re in that state, and there’s 3 directions for you to take (a, b, or c).
You call yourself on [a], which gets marked as visited. Then [a], calls all of its adjacent nodes, one by one. Each one marks itself as visited, and before it returns, it marks it as unvisited. So after your call on [a], your array of booleans (which you didn’t clone ever!), is in the same state as it was before the call. But you now have the longest path starting at [a]. Then you do the same for b and c, and return (to your parent caller), the longest of those three, and unmark your node as visited. Your parent caller does the same thing for all the other nodes adjacent to it, and returns to its parent, and so forth. It works.
However, even with this modification an exhaustive longest path search can be no more efficient than O(2n), making it unsuitable for anything but small maps. We must therefore find a way to estimate the longest path in quadratic (or linear, ideally) time. The other Concordia team accomplished this as follows:
[A.I Competition – Alexei/Andrew/Jason’s Algorithm]
Alexei explains once more:
On startup, we calculated the density of the map (how dense walls are vs. empty space.) Then we implemented two general purpose algorithms:
1. BFS: Breadth First Search to the enemy. Finds the shortest path to the enemy, and returns the first direction.
2. LongestPath (modified BFS): Finds which of the three directions would produce the largest open space. Essentially, 3 BFS searches are done, each one from scratch from each of the possible directions. However, instead of terminating when something is found, you instead count how many locations were traversed in total (the algorithm terminates when all reachable locations are traversed). Algorithm returns the direction that gives the highest such value.
In addition, the LongestPath was modified to not return a direction that would put us in a location to which the enemy could also move next turn, as otherwise this can cause a tie.
The idea is: At first, you want to advance the closest possible to the enemy, to “conquer” the most ground. After this, you want to take the direction that would produce the longest path.
Since we didn’t have time to code something that would detect when advancing BFS to the enemy would put us in a dead end path in the future (i.e. locking us and the enemy into a trap), the density check was necessary. On maps with lots of walls, like the chessboard – this situation could happen, so our AI just goes for LongestPath all the time there.
I’m really not sure how to go about analyzing their enemy chasing intelligence, other than to say that it sounds like a very good idea. When the wall density is low, following the longest path is less critical and it makes sense to try and restrict the amount of free space that the enemy has. This feature may very well have been their team’s winning edge. What is also remarkable about their algorithm, however, is how they went about searching for free space.
To reiterate, their team used a Breadth First Search, which is O(n), to estimate the longest path. Why is this an estimate? Because it fails to return the longest path (and therefore the theoretical best move) in every situation. Consider the following:
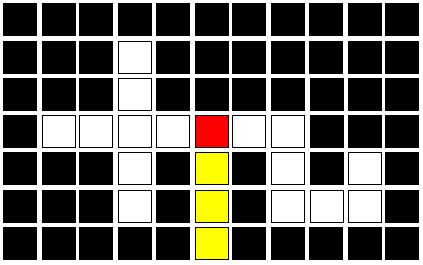
In this case, is it advantageous to turn right and survive for 7 turns. However, a modified BFS would choose to turn left, since there are a total of 8 free spaces as opposed to 7 on the right. The cycle would die sub-optimally in 4 turns. The same weakness is true for a modified depth-first search:

In this situation, the longest possible move is to turn left for 8 moves before dying. However, the modified DFS would return 6 for the right path and 5 for the left one, resulting in a disadvantageous right turn. Therefore, we can find specific situations where both BFS and DFS fail as estimators for the longest path.
Despite the shortcomings, I believe that estimating the longest path in this way is truly the most effective solution in a real time system. Since performing the exhaustive longest path search within the time constraints is impossible on a medium or large sized map, we must settle for using reasonable estimators. The modified BFS and DFS both do a very good job of measuring free space, each in a slightly different way.




